 |
Prof. Mg. Horacio Daniel Salomone * Los asteroides troyanos son cuerpos menores que se ubican en zonas especiales de la órbita de un planeta, sin alterar su movimiento alrededor del Sol. Esas zonas se conocen como puntos de Lagrange. |
Puntos de Lagrange: el lugar de descanso de Asteroides Troyanos y Telescopios Espaciales
Los asteroides troyanos son el resultado de la interacción gravitatoria entre dos cuerpos que tengan masas muy grandes y órbitas aproximadamente circulares con un tercer cuerpo (llamado comúnmente planetoide o en este caso asteroide troyano) de masa despreciable, que no afecte la órbita de los otros dos. En el Sistema Solar existen miles de cuerpos menores que interactúan con el Sol y los planetas, de los cuales, se denomina “asteroide troyano” a aquellos cuerpos que se encuentran en los puntos de Lagrange L4 y L5 de la órbita de un planeta. Los puntos de Lagrange son posiciones en la configuración orbital de dos cuerpos muy masivos donde un planetoide, que se vea afectado solo por la gravedad, puede mantener una posición estable en relación a ambos objetos. Es decir, son puntos donde la atracción gravitacional combinada de ambas masas, proporciona la fuerza centrípeta necesaria para que orbite con ellos, al mismo ritmo, en lugar de pasar a una órbita propia entorno a cualquiera de ellos.

Asteroides Troyanos cercanos a Júpiter (imagen ilustrativa)
Para poder estudiar la ubicación de los llamados asteroides troyanos, debemos primeramente analizar el llamado “problema restringido de los tres cuerpos”. Este problema consiste en hallar la solución general del movimiento de tres cuerpos que interactúan con la ley de gravitación de Newton. Este problema resulta de gran importancia en mecánica por su dificultad y puede analizarse de manera aproximada bajo las siguientes condiciones:
1) Dos de los cuerpos son de gran masa, por ejemplo el Sol y un planeta, y poseen órbitas circulares.
2) El tercer cuerpo es de masa despreciable frente a los otros dos, llamado comúnmente planetoide, de manera que no afecte el movimiento de los otros dos.
Esta formulación del "problema restringido de los tres cuerpos”, es una primera aproximación para describir el movimiento de un satélite alrededor de un planeta y el Sol, o de un asteroide bajo la influencia de un planeta y el Sol.
Pueden obtenerse importantes conclusiones en forma cualitativa, trabajando en un sistema de referencia que rota con la velocidad angular del sistema de los dos cuerpos principales. Deben tenerse en cuenta las energías potenciales (potenciales gravitacionales de los cuerpos) y cinéticas (traslaciones y rotaciones) para poder escribir adecuadamente, lo que en física se conoce como, el Lagrangeano del tercer cuerpo, una función escalar (no vectorial) que permite calcular la evolución temporal de un sistema.
Normalmente al hacer esto se obtiene una ecuación lagrangeana que no depende del tiempo, en la que se conserva una cantidad física que recibe el nombre de integral de Jacobi. La conservación de esta última cantidad es completamente análoga a pedir que en el sistema restringido de los tres cuerpos la energía del mismo se conserve y la misma puede ser utilizada para hacer un análisis cualitativo del movimiento. Cuando el movimiento del planetoide (tercer cuerpo) se encuentra en el plano orbital de los otros dos objetos masivos, el movimiento se encuentra restringido y la integral de Jacobi queda reducida a una ecuación cuadrática (si, como las que normalmente nos enseñan a resolver en la escuela secundaria) … A partir de esto, pueden obtenerse las curvas de velocidad del planetoide.
Un punto en el plano orbital que queda definido por los dos objetos masivos es de equilibrio relativo si al situar en este punto al planetoide (tercer cuerpo) con velocidad cero, éste permanece en dicho punto. Al resolver el problema anterior, se sabe que hay cinco y sólo cinco puntos de equilibrio relativo, las dos posiciones L4 y L5 de Lagrange, en las que el tercer cuerpo está en los vértices de un triángulo equilátero, y las tres posiciones colineales L1, L2 y L3 de Euler. A estos cinco puntos, se les da el nombre de “puntos de Lagrange”. Dichos puntos se muestran a continuación. En el sistema no rotado veríamos que las tres masas avanzan con la misma velocidad angular en sus órbitas circulares.
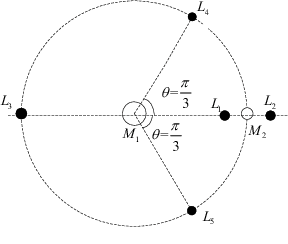
A continuación, se muestran en un diagrama las curvas de velocidad cero para el caso del problema restringido de los tres cuerpos, es decir, cuando el tercer cuerpo es mucho menor que los otros dos, en este caso podríamos hablar de un Asteroide Troyano o un satélite respecto del sistema Sol-Tierra. El movimiento de un satélite próximo a la Tierra, queda confinado a la región comprendida en la zona que la rodea a ella. Los valles “encima y debajo” del Sol y la Tierra corresponden a órbitas potencialmente inestables. Sin embargo, la presencia de fuerzas de Coriolis estabiliza en ciertas circunstancias el movimiento. Las flechas rojas y azules indican gradientes para las zonas anteriormente descriptas.
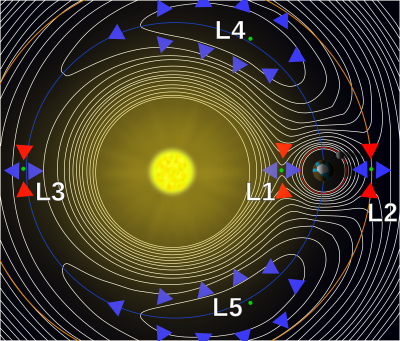
Los puntos de Lagrange L1, L2 y L3 se tratan de puntos de equilibrio inestables. Por otra parte, en los valles situados encima y debajo de los cuerpos principales, hay dos mínimos que son también puntos de equilibrio, pero éstos son estables. No es difícil probar que L4 y L5 están en los vértices de dos triángulos equiláteros iguales, cuyas bases son el segmento de recta que une al Sol con la Tierra.
Al determinar la ubicación y estabilidad de los puntos de Lagrange, resulta de mucha utilidad estudiar las oscilaciones que se producen en torno a estos puntos de equilibrio dado que son observadas en el movimiento de los asteroides troyanos. El sistema posee dos modos normales de oscilación, similares a los modos de oscilación de un resorte pero para el movimiento del planetoide. Estos modos de oscilación poseen frecuencias muy específicas, situación en la cual representan un movimiento oscilatorio estable alrededor del punto de equilibrio L4 o L5. Se puede observar que las frecuencias de oscilación corresponden a dos modos normales del sistema en los cuales se produce una oscilación en la dirección radial que provoca una excentricidad de la órbita y una oscilación en la dirección casi perpendicular a la radial que produce un movimiento de libración.
Durante mucho tiempo los únicos asteroides troyanos conocidos fueron los de Júpiter (técnicamente solo los que se encuentran en L4 se llaman troyanos, mientras que los de L5 son ‘griegos’ o ‘aqueos’ siguiendo con una nomenclatura basada en La Ilíada de Homero). Los troyanos de Júpiter constituyen una familia de miles de cuerpos que compite en número con el cinturón principal de asteroides ubicado entre los planetas Marte y Júpiter. El primer troyano de Júpiter, 588 Aquiles, se descubrió en 1906 y durante mucho tiempo se pensó que estos asteroides eran una característica exclusiva del gigante joviano, como una consecuencia de su gran campo gravitatorio.
La existencia de asteroides troyanos en otros planetas se consideraba prácticamente imposible porque las órbitas serían extremadamente inestables. Sin embargo, en las últimas décadas se ha descubierto que casi todos los planetas están acompañados de troyanos. Venus, la Tierra, Marte, Urano y Neptuno tienen su propio conjunto de cuerpos situados en los puntos de Lagrange L4 y L5, aunque en un número mucho menor que los que posee Júpiter. Tanto Venus como la Tierra poseen pocos troyanos y son muy inestables (solo conocemos un asteroide troyano de la Tierra, 2010 TK7), mientras que Neptuno, que se halla lejos de Júpiter y cerca del cinturón de Kuiper, debe contar con una población relativamente numerosa y estable (hay catalogados hasta el momento 17 asteroides troyanos de Neptuno). Hasta la fecha no se ha descubierto ningún troyano de Saturno, cuya proximidad a Júpiter es un factor negativo de cara a la estabilidad de estos cuerpos, aunque con toda seguridad tendrá varios de carácter temporal.
Lo más llamativo es la existencia de troyanos de Marte. Si combinamos la escasa gravedad de Marte con su cercanía a Júpiter el resultado debería ser la ausencia de troyanos del planeta rojo, sin embargo, se han descubierto nueve troyanos marcianos (ocho en L5 y uno en L4), el tercer grupo más numeroso tras los de Júpiter y Neptuno. La mayoría de ellos tienen órbitas estables. Una posibilidad, es que sean pedazos del propio Marte, es decir, restos de su formación, del mismo modo que nuestra Luna fue el resultado de la colisión de la proto-Tierra con el protoplaneta Theia. El troyano marciano más grande es 5261 Eureka, que fue descubierto en 1990 en el punto L5 de la órbita marciana. Lo particular es que otros seis de los troyanos marcianos se hallan en la misma zona y muestran similitudes con Eureka, de ahí que se les considere miembros de un mismo grupo que recibe el nombre, lógicamente, de asteroides tipo Eureka.
Por otra parte, el primer asteroide troyano de la Tierra se descubrió en octubre de 2010 por la NASA y fue bautizado como 2010 TK7. Éste asteroide oscila alrededor del punto de Lagrange L4 del sistema Sol-Tierra. El asteroide se encuentra ubicado a unos 80 millones de kilómetros de la Tierra.
En cuanto a los puntos de Lagrange L1 y L2 de la Tierra, se tratan de puntos inestables pero revisten una gran utilidad para la astronomía espacial. Dichos puntos resultan lugares óptimos para la colocación de telescopios espaciales. El punto L1, nunca recibe sombra de la Tierra ni de la Luna, lo que lo convierte en un lugar ideal para colocar instrumentos de observación solar. Allí se han colocado el Observatorio Solar y Heliosférico (SOHO), el Advanced Composition Explorer (ACE) y el WIND. En L2, apuntando hacia el otro lado está el WMAP y los observatorios Herschel y Planck, así como también el sucesor del Hubble, el telescopio espacial James Webb (mostrado en la siguiente imagen). El punto L3 de la Tierra es muy inestable (más aún que L1 y L2, por acción gravitatoria de Venus) pero tiene un halo de misterio al encontrarse al otro lado del Sol. A lo largo de la historia de la literatura de ciencia ficción ha sido un lugar favorito para esconder una “anti-Tierra” tanto así como naves espaciales alienígenas.

El Telescopio Espacial James Webb, se encuentra en el punto de Lagrange L2 de la Tierra
(*) Prof. Mg. Horacio D. Salomone
IDEI, Área Ciencia y Tecnologías Básicas - UNGS
FAIN, Departamento de Ciencias Básicas - UADE